1、 FM背景

在进行CTR预估时，除了单特征外，往往要对特征进行组合。对于特征组合来说，业界现在通用的做法主要有两大类：FM系列与Tree系列。今天，我们就来讲讲FM算法。

FM 解决one-hot特征稀疏的问题

FM(Factorization Machine)主要是为了解决数据稀疏的情况下，特征怎样组合的问题。已一个广告分类的问题为例，根据用户与广告位的一些特征，来预测用户是否会点击广告。数据如下：(本例来自美团技术团队分享的paper)

Clicked?	Country	Day	Ad_type
1	USA	26/11/15	Movie
0	China	1/7/14	Game
1	China	19/2/15	Game

“Clicked?”是label，Country、Day、Ad_type是特征。由于三种特征都是categorical类型的，需要经过独热编码（One-Hot Encoding）转换成数值型特征。

因为是categorical特征，所以经过one-hot编码以后，不可避免的样本的数据就变得很稀疏。举个非常简单的例子，假设淘宝或者京东上的item为100万，如果对item这个维度进行one-hot编码，光这一个维度数据的稀疏度就是百万分之一。由此可见，数据的稀疏性，是我们在实际应用场景中面临的一个非常常见的挑战与问题。

one-hot编码带来的另一个问题是特征空间变大。同样以上面淘宝上的item为例，将item进行one-hot编码以后，样本空间有一个categorical变为了百万维的数值特征，特征空间一下子暴增一百万。所以大厂动不动上亿维度，就是这么来的。

FM

FM模型用n个隐变量来刻画特征之间的交互关系。这里要强调的一点是，n是特征的总数，是one-hot展开之后的，比如有三组特征，两个连续特征，一个离散特征有5个取值，那么n=7而不是n=3.

FM 公式

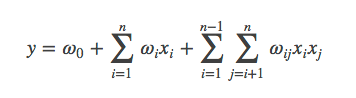
上式中，n表示样本的特征数量,xi表示第i个特征。
与线性模型相比，FM的模型就多了后面特征组合的部分。

从上面的式子可以很容易看出，组合部分的特征相关参数共有n(n−1)/2个。但是如第二部分所分析，在数据很稀疏的情况下，满足xi,xj都不为0的情况非常少，这样将导致ωij无法通过训练得出。

为了求出ωij，我们对每一个特征分量xi引入辅助向量Vi=(vi1,vi2,⋯,vik)。然后，利用$v_iv_j^T$对$ω_{ij}$进行求解。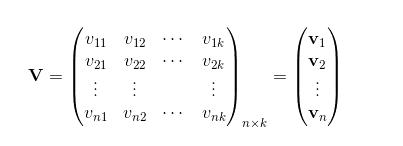

那么ωij组成的矩阵可以表示为: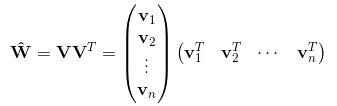

那么，如何求解vi和vj呢？主要采用了公式：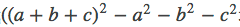

具体过程如下：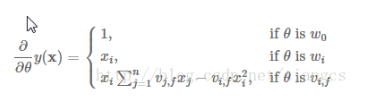

经过这样的分解之后，我们就可以通过随机梯度下降SGD进行求解：

KDD2018 论文对FM构建特征交叉的评价

KDD 2018 微软论文：

从特征构建的层面而言，现阶段深度学习技术在推荐系统中的应用可以大致分为两类：

（1）从原始数据中自动学习出蕴含语义的隐特征，例如从本文、图像或者知识网络中提取出有效的隐特征；

（2）自动学习多个相关特征之间的交互关系。

特征交互指的是学习两个或多个原始特征之间的交叉组合。例如，经典的基于模型的协同过滤其实是在学习二阶的交叉特征，即学习二元组[user_id, item_id]的联系。而当输入数据的内容变得丰富时，就需要高阶的交叉特征，例如，在新闻推荐场景中，一个三阶交叉特征为AND(user_organization=msra,item_category=deeplearning,time=monday_morning) , 它表示当前用户的工作单位为微软亚洲研究院，当前文章的类别是与深度学习相关的，并且推送时间是周一上午。

传统的推荐系统中，高阶交叉特征通常是由工程师手工提取的，这种做法主要有三种缺点：

（1）重要的特征都是与应用场景息息相关的，针对每一种应用场景，工程师们都需要首先花费大量时间和精力深入了解数据的规律之后才能设计、提取出高效的高阶交叉特征，因此人力成本高昂；

（2）原始数据中往往包含大量稀疏的特征，例如用户和物品的ID，交叉特征的维度空间是原始特征维度的乘积，因此很容易带来维度灾难的问题；

（3）人工提取的交叉特征无法泛化到未曾在训练样本中出现过的模式中。

因此自动学习特征间的交互关系是十分有意义的。目前大部分相关的研究工作是基于因子分解机的框架，利用多层全连接神经网络去自动学习特征间的高阶交互关系，例如FNN、PNN和DeepFM等。其缺点是模型学习出的是隐式的交互特征，其形式是未知的、不可控的；同时它们的特征交互是发生在元素级（bit-wise）而不是特征向量之间（vector-wise），这一点违背了因子分解机的初衷。来自Google的团队在KDD 2017 AdKDD & TargetAD研讨会上提出了DCN模型，旨在显式地学习高阶特征交互，其优点是模型非常轻巧高效，但缺点是最终模型的表现形式是一种很特殊的向量扩张，同时特征交互依旧是发生在元素级上。

参考资料

美团点评《深入FFM原理与实践》
https://tech.meituan.com/deep_understanding_of_ffm_principles_and_practices.html

《推荐系统遇上深度学习(一)—FM模型理论和实践》https://www.jianshu.com/p/152ae633fb00

《第09章：深入浅出ML之Factorization家族》
http://www.52caml.com/head_first_ml/ml-chapter9-factorization-family/